SPIの試験に続いて、次に受けた企業では一次面接通過のお知らせと共に、WEB適性検査の案内が。。。この企業も、一週間以内の受験依頼です。
今回も、インターネットの情報から、急ぎ対策をしたいと思います。新型といわれる試験は対策の必要はなさそうですが、従来型といわれる試験は難しいので、対策が必要そうです。私が受けている企業がどちらを採用しているか不明なので、従来型に備えたいと思います!
今回は、「TG-WEBマスター」とやらが運営するサイトを参考に準備をしていきたいと思います。
時間がないので、暗記すべきポイントをピックアップして、直前にインプットするという方法で乗り切りたいと思います。
<従来型>
| 科目 | 試験時間 | 問題数 | 出題内容 |
|---|---|---|---|
| 言語 | 12分 | 12問 | 空欄補充、並び替え、長文読解 |
| 計数 | 18分 | 9問 | 図形、推論、暗号、命題、数列など |
| 英語 | 15分 | 10問 | 長文読解 |
| 性格検査 | 企業によって異なる | 同左 | 同左 |
<新型>
| 科目 | 試験時間 | 問題数 | 出題内容 |
|---|---|---|---|
| 言語 | 7分 | 34問 | 同義語・対義語、ことわざ、慣用句、四字熟語、長文読解 |
| 計数 | 8分 | 36問 | 四則逆算、図表の読み取り |
| 英語 | 15分 | 10問 | 長文読解 |
| 性格検査 | 企業によって異なる | 同左 | 同左 |
立方体と正八面体の展開図
立方体の展開図(全11種類)
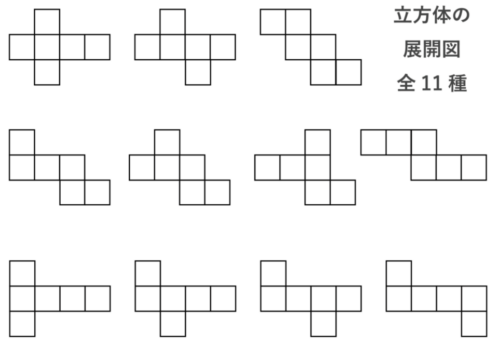
正八面体の展開図(全11種類)
正八面体とは、8つの正三角形から成り立つ立体。
面は8つ、辺の数は12本、頂点は6つ。1つの頂点に4つの辺が集まっている構造
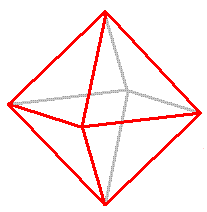
パターンは3つ:
①6つの正三角形が並ぶ形
②5つの正三角形が並ぶ形
③4つの正三角形が並ぶ形
①6つの正三角形が並ぶ形(同一色は、正八面体に組み立てた際に平行な面)
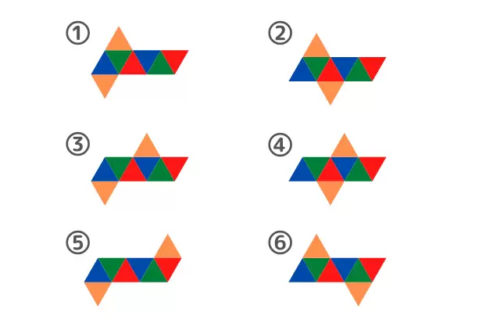
②5つの正三角形が並ぶ形
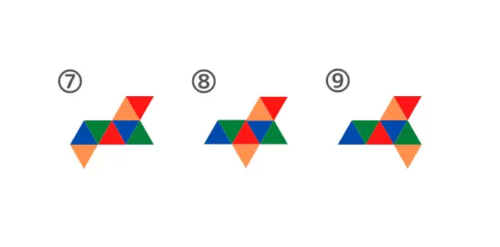
③4つの正三角形が並ぶ形

正多面体の面の形と辺の数・頂点の数を求める公式
正多面体の辺の数:「1つの面の辺の数×面の数÷2」
正多面体の頂点の数:「辺の数-面の数+2」
| 正多面体の種類 | 面の形 | 面の数 | 辺の数 | 頂点の数 |
|---|---|---|---|---|
| 正四面体 | 正三角形 | 4 | 6 | 4 |
| 正六面体/立方体 | 正方形 | 6 | 12 | 8 |
| 正八面体 | 正三角形 | 8 | 12 | 6 |
| 正十二面体 | 正五角形 | 12 | 30 | 20 |
| 正二十面体 | 正三角形 | 20 | 30 | 12 |
三段論法
三段論法とは「AならばB」と「BならばC」が成り立つとき、「AならばC」が成り立つことです。
・命題P「AならばB」に対して、
・「BならばA」をPの逆
・「AでないならばBでない」をPの裏
・「BでないならばAでない」を対偶
命題とその対偶の真偽は必ず一致します。
また、命題の裏は逆の対偶なので、逆と裏の真偽も必ず一致。
一筆書き:「奇点が0個(遇点のみ)または奇点が2個」の時
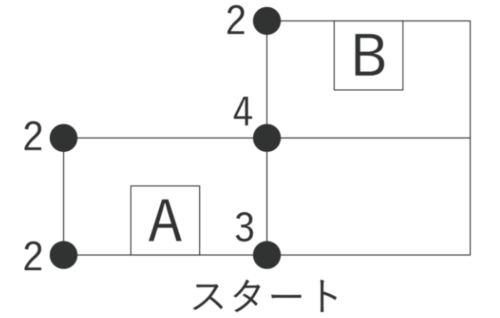
曲がり角や交差点などの「点」に線が何本集まっているかを数えたとき、点に集まる線が奇数本のときは「奇点」、偶数本のときは「偶点」と呼びます。
以下の図だと2と4は偶点、3は奇点。奇点が0個の場合、どの点からスタートしても、元の点に戻れます。奇点が2個の場合、奇点からスタートして、もう1個の奇点がゴールとなります。
(例題)正方形、正五角形、正六角形、正七角形、正八角形・・・正十二角形、正十三角形に対角線をすべて書き込んだ場合、これら10個の図形のうち、一筆書きできるものはいくつあるか?
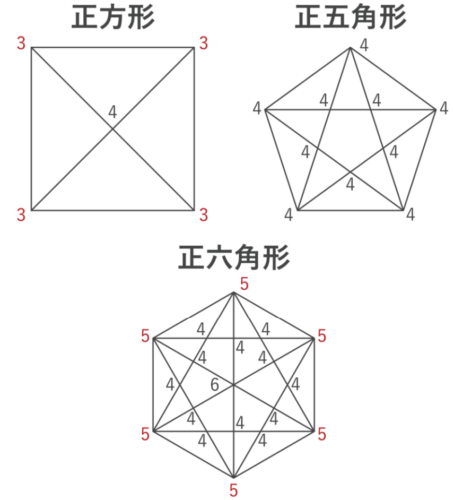
- 正方形=奇点が4個なので、一筆書きできない
- 正五角形=奇点が0個なので、一筆書きできる
- 正六角形=奇点が6個なので、一筆書きできない
各頂点に集まる線の数は「多角形の角数-1」なので、正方形は3、正五角形は4、正六角形は5・・・となります。
各頂点に集まる線の数が偶数(偶点)なら「奇点=0個」となり、一筆書きができます。
あてはまるのは多角形の角数=奇数のときなので、正五角形・正七角形・正九角形・正十一角形・正十三角形の5つとなります。
その他
1人あたりのGDP=GDP÷人口
人口密度=人口/面積(人口=面積×人口密度)
最後に
上記に加えて、週明けを予定している試験当日迄に、暗記すべきポイントを順次アップデートしていきたいと思います!
兎にも角にも、試験前は頭すっきりの状態で受験をできる様に、前日は睡眠を良くとり、当日はカフェインをたっぷりと取る様にすることが重要だと思います。


